深度|自动做市商（AMM）算法、现状和未来发展的探索

在本文中，我们将首先回顾由Bancor、Uniswap、balancer和curve协议实现的四种自动做市商（AMM）算法。还将讨论AMM算法的**发展、可能的改进和未来。

Bancor Network 的联合曲线概念和交易公式:

Bancor¹利用联合曲线的概念来确定价格。联合曲线是代币价格与其总供应量之间的关系。

Bancor协议通过智能合约为加密代币提供持续流动性

https://storage.googleapis.com/website-bancor/2018/04/01ba8253-bancor_protocol_whitepaper_en.pdf

联合曲线 Bonding Curve：

联合曲线模可以理解为描述“代币买卖价格”和“代币发行总量”之间的函数关系，智能合约可以以去中心化的方式自动执行。

https://medium.com/linum-labs/intro-to-bonding-curves-and-shapes-bf326bc4e11a

Bancor网络选择的不变量为f，称为连接权。在第一个表达式中，R表示流动性池中储备代币的数量，s表示流动性池外BNT的总供应量，P表示BNT和储备代币的相对价格。我们可以代入P的方程，对两边积分，得到P和S之间的关系。这是一个指数表达式，其中指数α与连接权重f相关（f介于0和1之间）。F越小，α越大，这意味着相对于BNT的总供应量，价格变化更快。

两边积分

Formulas for Bancor system

https://drive.google.com/file/d/0B3HPNP-GDn7aRkVaV3dkVl9NS2M/view?resourcekey=0 -MBIGRD0B9H8DPNRAEB_Uta

使用这个表达式和一个简单的积分，我们可以导出T（购买的BNT代币）和E（支付的备用代币）之间的关系，其中R0和S0是R和s的当前值。

如果我们想在代币a和代币B之间交换，我们将代币a出售给代币B。我们首先需要使用代币a从池a购买BNT代币（注意：如果我们没有BNT代币）。接下来，我们需要使用BNT从池B购买代币B。下面是计算我们将收到多少代币所需的精确公式。代币a和代币B之间的相对价格可以表示为BNT代币和代币a/B之间的相对价格。

优点：Bancor允许在某些池中单方面注入流动性，这由Bancor治理决定，单边流动性可存多少是有限的，这也取决于Bancor治理。在限额内，当用户以其他代币形式存入单边流动性时，Bancor将补充同等的BNT代币。这使得用户提供的有效移动性增加了一倍。如果达到限额，如果人们想要存入单边流动性，他们必须等待有人提取单边流动性，或者有人使用BNT作为单边流动性注入。

Bancor协议补偿用户在将单边流动性存入BNT赚取的佣金（稍后将讨论）时的非**性损失。如果交易成本无法完全补偿非**性损失，Bancor将铸造BNT，以确保非**性损失为零。因此，如果流动性提供者将其流动性存入一段时间（100天后可以全额补偿），他们可以享受稳定的收入。

缺点：如上所述，所有交易都需要BNT代币作为中介。因此，我们将经历两个滑动点。出于同样的原因，所有流动性池都由BNT和另一种代币组成，因此缺乏多样性。BNT代币价格也可能受到影响，因为实现非**性损失补偿和单边流动性存款需要灵活的供应。

Bancor引入了连通代币BNT的概念，它将所有具有不同连接权重的代币连接起来，并对应于决定价格的不同联合曲线。

Uniswap 的无常损失计算:

Uniswap使用固定产品做市商（CPMM）来确定价格。在深入研究Uniswap V2和V3使用的算法之前，让我们先了解什么是无常损耗（IL）以及如何计算它。

固定产品做市商（CPMM）

固定产品做市商

两项资产储备的乘积必须始终保持不变x*y=K，这是强制性的

https://ETHresear.ch/t/improving-front-running-resistance-of-x-y-k-market-makers/1281

无常损失

无常损失指流动性池中的资金损失。

https://finematics.com/impermanent-loss-explained/

如果AMM函数是凸函数（注：价格随买入而上涨/随卖出而下跌），没有交易成本补偿的单一交易将始终导致流动性提供者赔钱。假设一个事务导致AMM函数从点1移动到点2。第1点和第2点（函数导数的**值）的现货价格为P1和P2。P3为实际交易价格。由于凸函数的性质，P1gt;；P3gt;；P2.非**性损失定义为交易后池中流动性提供者代币的现值与流动性提供者代币的现值之间的差额。如果他只持有代币，不使用代币提供流动性，则表示为V和vheld。为方便起见，无常损失和价格将以代币y表示（1代币y的价格为单位1）。经过一些简单的推导，很容易证明非**性损耗始终小于零（x2 gt; x1，P2 lt; P3）。

Uniswap³V2使用一个简单但功能强大的公式来确定事务。池中代币保留的数量的乘积是常数。与Bancor相比，它摆脱了连接代币的依赖性。交易完全由流动性池中代币的数量决定。

Uniswap³

Uniswap V2核心

https://Uniswap.org/whitepaper.pdf

由于此函数的性质，池中两个代币的价值将始终相同（本文中使用的价格将始终是相对价格）。

使用相同的逻辑，不难计算Uniswap v2中单个非手续费的非**性损失。假设交易将价格从P更改为PK。以百分比形式测量的非**性损失可单独表示为K的函数。

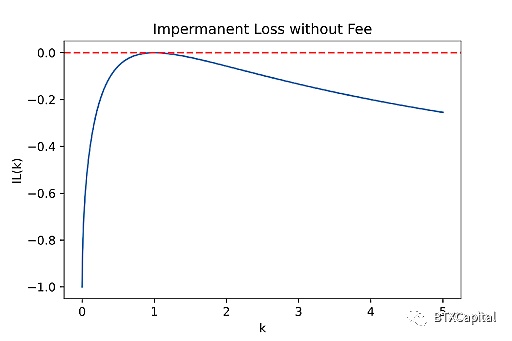
毫不奇怪，这个函数总是小于或等于零，正如我们可以从上面的无成本非**损失图中看到的那样。如果水平轴在对数空间中绘制，则IL（k）将是对称的。结论是：相对价格变动越大，短期损失越大。这可以通过以下事实来解释：流动性提供者的更有价值的代币从池中购买，留下更多价值更低的代币。

当价格变动在2ρ之间时的正向收益:

接下来，让我们看看如果我们增加交易费用，IL（k）将如何表现：

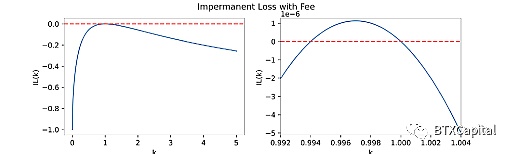
导出的非**性损失函数IL（k，ρ）看起来非常类似于无代价非**性损失函数ρ设置为零进行合理性验证，并得到相同的结果。典的Uniswap V2费用百分比为ρ=0.3%。在绘制无常损失函数时，我们可以看到，在大约k=0.994到1（大约2ρSpan）中。在该地区，非**性损失为正，这意味着流动性提供者实际获得了价值（该地区赚取的交易费优于损失）。通过引入交易费用，当价格在一定范围内波动时，流动性提供者将获得正回报。

当价格变化更加不稳定时，流动性提供者似乎总是赔钱。然而，情况并非如此。我们知道Dave white4和其他人已经解决了这个问题。不幸的是，这超出了本介绍性文件的范围。我们打算在将来进一步研究这个问题。

Dave White4

Uniswap’s Financial Alchemy

https://research.paradigm.xyz/Uniswaps-alchemy

至于其他流行的AMM算法（包括Uniswap V3）的无常损失的推导，我们推荐Xu Jiahua的这篇论文⁵ 这些推导将是下一次的主题。

Jiahua Xu⁵

SoK: Decentralized Exchanges (DEX) with Automated Market Maker (AMM) protocols

https://arxiv.org/abs/2103.12732

优点：第一种方法使用池中代币数量的凸函数来确定价格。

缺点：流动性供应在所有价格范围内均匀分布，这意味着资本效率较低。

流动性分布、流动性注入、Uniswap V3 范围订单:

为了提高流动性效用并降低波动性损失的风险，Uniswap⁶ V3允许用户仅在特定价格范围内提供流动性。

Uniswap⁶

Uniswap V3核心

https://Uniswap.org/whitepaper-v3.pdf

来自Uniswap V3白皮书

这是通过转换Uniswap V2功能实现的：

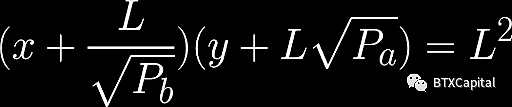
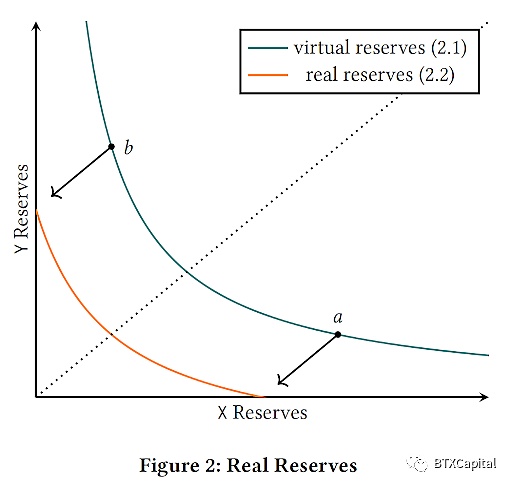
来自Uniswap V3白皮书

将函数向下平移到a点的y值，向左平移到B点的x值，如上图和等式所示，以确保a和B之间的有效交易结果，就像我们使用绿色曲线作为价格确定函数一样。当价格超过该范围时，其中一个代币储备将被出售，有效地将流动性集中在该价格范围内。

丹罗宾逊⁷ （注：paradim风险投资基金研究员总监）发表了一篇关于计算多个AMM流动性分布的**论文。

Dan Robinson⁷

Uniswap V3: The Universal AMM

https://www.paradigm.xyz/2021/06/Uniswap-v3-the-universal-amm/

也可以简单地证明，相同价格范围内两个流动性提供者的流动性可以简单地相加。

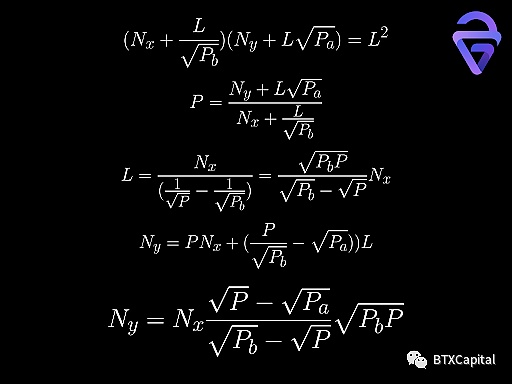
如上所示，在存放流动性时，Uniswap V3中每项资产的价值不一定相等。只有当p等于PA和Pb的几何平均值时，每项资产的价值才相等。当p小于几何平均值时，资产x的值大于资产y的值。当p大于几何平均值时，资产x的值小于资产y的值。

当当前价格完全超过流动性提供者设置的价格范围时，Uniswap V3将流动性提供者的输入计算为范围订单，并允许其仅存款一个代币（类取决于价格范围是否完全高于或低于当前价格）。例如，考虑由ETS和戴组成的流动性池。如果设定的价格范围完全高于ETH的当前价格，则仅允许用户存入ETH。如果价格范围完全低于ETH的当前价格，则仅允许用户存入Dai。当价格完全超过流动性提供者设定的价格范围时，他存入的所有资产将转换为另一种代币。由于用户只能存入一个代币，范围订单只能实现传统限价订单（利润订单和购买限价订单）的四分之二。另一方面，购买止损单和止损单无法实现。到目前为止，我们还不知道限制作用域顺序代币类的目的是什么。

范围订单

RangeOrders

本质上并不是真正的订单，而是 LP 向资金池某个特定价格点提供的聚合流动性。虽然不是真正的订单，但「范围订单」所表现出的特性，却很好地模拟了限价单的基本功能。

https://docs.Uniswap.org/protocol/concepts/V3-overview/range-orders

优点：Uniswap V3引入了流动性分配的概念，允许用户在价格范围内存储流动性。通过集中流动性提高资本效率。当存放相同价值的资产时，可以获得较高的流动性和较低的滑动点。在一定价格范围内提供流动性也在一定程度上降低了非**性损失的风险。

缺点：用户在进行范围订单时只能存放某些类的代币。因此，无法实现买入止损单和止损单。

Uniswap V2和V3在AMM算法中引入了CPMM和流动性分配。在价格范围内提供流动性基本上使Uniswap V3成为通用AMM，通过改变其流动性分布，它可以成为任何可能的AMM。

Balancer 的做市函数和交易公式:

Balancer⁸ 将Uniswap V2的双代币池扩展为多代币池。Balancer池中每个资产的值都具有恒定的权重，加起来等于1。不难证明每项资产储量的幂积是常数。资产n相对于资产t的价格也可以导出为资产t和n的储量之间的比率，该比率通过其权重标准化。

Balancer⁸

A non-custodial portfolio manager, liquidity provider, and price sensor

https://balancer.fi/whitepaper.pdf

基于常量不变量，我们可以导出具有不同输入值的事务公式（资产O和资产I之间的事务）。在本符号标准中，资产o始终是购买的资产。资产I是出售的资产。A和B是输入/接收的代币数和当前代币保留。我们还可以根据价格变化计算输入或购买的代币数量。

智能订单路由（SOR）算法：

Balancer 还引入了智能订单路由(SOR⁹) 算法。

SOR⁹

art Order Router V2

https://docs.balancer.fi/developers/art-order-router

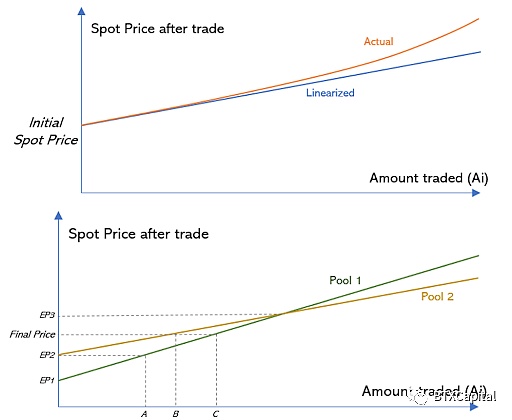
资料来源：https://docs.balancer.fi/v/v1/art-contracts/sor/

该算法的总体思想是将一个订单分成几个小块，在不同的Balancer池中进行交易，以获得更好的交易结果。假设我们想要在代币池1和代币池2中进行交易。如果我们想要交易的总金额n低于上图中的a，我们将只在代币池1中进行交易，因为tok的价格en池1始终优于代币池2。如果总金额超过a，我们将在代币池1中交易一些订单，在代币池2中交易一些订单。每个代币池中的交易数量将使每个池中的价格相等（B+C=n）。

很容易证明**策略总是使每个池中的价格相等（如果价格不相等，我们总能找到更好的池来改善我们的交易结果）。

相对于交易量的价格函数通常是非线性函数。Balancer将价格函数简化为线性函数。如果存在n个代币池，则**策略可以表示为：

如果剩余价格函数的价格函数始终大于或小于范围（0，n），则应从上述计算中删除价格函数和相应的池，以确保结果有效。如果价格函数始终很小，显然**的策略是交换池中的所有代币。

在此计算中，未考虑天然气成本。事实上，**策略应该是在路由收入和天然气成本损失之间保持平衡。

SOR算法，我们相信，可以在更广泛的背景下使用。例如，价格函数可以是其他AMM协议池的函数。由于我们现有知识的限制，我们不确定实际的AMM聚合器是否使用相同的逻辑来实现更好的价格。没有任何价格函数近似的更通用的解决方案n将在本文后面讨论。

优点：balancer将两个代币池扩展到多个代币池，并引入sor算法，为用户提供更好的价格。

缺点：“流动性池的强度取决于其最弱的资产。”池中的代币类越多，风险越高。

Balancer是一种多代币投资组合管理工具，它允许灵活的代币价值分配，并具有价格优化算法。